Zappos COO Alfred Lin enlightens us on how to become 37 times more productive in only one year! Can it be? Let’s hear him out:

Make at least one improvement [every day] that makes Zappos better. It sounds daunting, but remember improvements don’t have to be dramatic. Think about what it means to improve just 1% per day and build upon that every single day. Doing so has a dramatic effect and will make us 37x better, not 365% (3.65x) better at the end of the year. Wake up every day and ask yourself not only what is the 1% improvement I can change to make Zappos better, but also what is the 1% improvement I can change to make myself better personally and professionally — because we, Zappos, can’t grow unless we as individual people grow too.
Imagine yourself making 1% changes every day that compounds and will make you and Zappos 37x better by the end of the year. Imagine if every employee at Zappos was doing the same. Imagine how much better you, Zappos and the world will be next year.
At first glance it’s inspiring. At second glace it’s poppycock. At third glance you wonder how it’s possible for someone to use the word “Zappos” so frequently.
Being 37x more productive is impossible, and I’ll show you why. But along the way it will become clear how becoming 2-3x more productive might be within reach.
His math isn’t the problem per se. It’s true that if you improve 1% each day over the previous day, that’s a 1% compounding rate. My question is: Is it possible to increase your daily productivity by an entire percent every day?
To answer that, I want to give you a fun math puzzle. Yeah, I know, “fun” is relative… Okay look if you don’t like word problems just take a random guess at the answer. If you’re up for the challenge, try to solve it without pen and paper. You know, just to prove your MIT education wasn’t for nothing.
Here’s the puzzle: You get in your car at home and head out towards your mother’s house 60 miles away. (Your mom likes this word problem, I can already tell.) You hit traffic during the first half of the trip, so after 30 miles you’ve averaged only 30 miles per hour.
Now the traffic opens up and you can go as fast as you want. The question is: How fast do you have to go during the second half of the trip such that you’ve averaged 60 mph over the entire trip?
If you’re not using pen and paper, maybe you guessed 90? 120?
Actually it’s impossible! To average 60 mph you need to travel the whole 60 miles in a single hour. But it’s already been an hour! Even if you went 1000 mph during the second half, it would have taken just over an hour to complete the 60 miles, therefore your average is still less than 60 mph.
It’s amazing how periods of low velocity wash away gains of high velocity. In the puzzle, if you doubled your speed in the second half it would increase your trip average from 30 to 40 mph. If you quadrupled your speed in the second half, your trip average would still be only 48 mph.
Once you’re behind, you can’t make up ground no matter how fast you go.
This puzzle illustrates the weird math of velocities, and what applies to “miles” per hour also applies to emails per hour or writing code or writing prose or any other “gettin’ stuff done” per hour.
The problem with improving your productivity is that so much of your day is occupied by low-velocity activity — dealing with emails you didn’t really need to see, dawdling in a meeting that hasn’t started yet, or spending too much time reading blogs. (Present company excepted.)
When half your day moves at 30 mph, it’s impossible to make up the time during the other half.
This is the problem with Lin’s 1% idea — the low-velocity stuff makes it too difficult to improve even 1% overall, at least not every day of the year. Even with 37x improvement in some areas, you still might not be 2x more productive overall.
There’s good news here, however! Once you realize that the low-velocity stuff is responsible for most of the drag on your productivity, you realize that the thing to do is eliminate the low-velocity stuff. Yes it’s good to learn to type faster, but cutting down on the time it takes to process useless email might help even more.
Ready for more good news? There are free tools that help you identify what the low-velocity stuff is. I use one called RescueTime. To show you how useful this is, consider this example of my stats for one week:
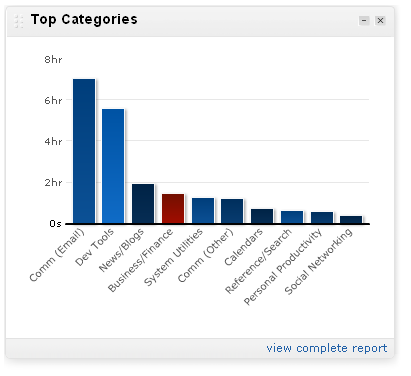
Whoa — almost eight hours of email. That’s a solid, uninterrupted, full day of nothing but email I’m blowing through every week. Is that really the way I should be spending the majority of my time?
Even the long tail can be instructive. Notice the 45 minutes of “Calendars.” A drill-down bears out the awful conclusion — yes I spent almost an hour in Google Calendar. It’s true this week was completely packed with events, but still.
Another realization: I had an averaged 5.5 hours of activity per day. I was in the office for over 8 hours every one of those days — the rest is sopped up with meetings, office chatter, and lunch. Here’s the mythical eight-hour workday quantified — I’m starting with 5-6 and even then I spent much of it fielding email.
Once you see the numbers it’s easy to correct. I now notice more when I’m in an office conversation that’s past the point of being productive. There’s millions of tips for how to process email more efficiently.
So if you’re serious about wanting to increase productivity by, say, 2x, you can. Identify the biggest perpetrators of low-velocity activity and eliminate them, then do a little surgery on your high-value tasks.
The best part is, none of this means working late or working harder. Just stop averaging down!
What are your tips for increasing productivity?
Leave a comment. It will be fun.
29 responses to “Double your productivity without more work or stress”
Your argument and math are correct, but you’ve taken Lin’s suggestion a bit out of context. Or rather, you’ve narrowed the context.
He said "improve just 1% per day". This doesn’t necessarily mean "be 1% more efficient". It could be 1% more sales, 1% lower expenses, 1% more efficient, 1% more happy customers, 1% fewer returns, 1% fewer defects, etc.
If you get too tied up in the math of it you miss the subjective/qualitative aspect of the original argument. I suspect the math is just there to dramatize the idea of continuous incremental improvement.
@Brian: I see your point, but Lin himself is caught up in the math. If he’s going to claim 37x improvement — based on math — then he’s opening himself up to a mathematical counterpoint.
Furthermore, I still disagree with your argument that it’s possible to improve "1% more sales" or "1% lower expenses" every day. I don’t believe you can, for example, improve sales by 37x in a year based on this advice. Do you?
<Math nitpick>
Your puzzle does not have enough information in the question. You need to specify "averaged over time" or "averaged over distance".
Averaged over time – It’s impossible to average 60 mph, as you say.
Averaged over distance – You need to drive 90 mph.
</Math nitpick>
Nice article. I just subscribed to your blog and enjoyed reading through the archives.
@Kyle: Thanks for the kind words!
I’m unsure of what you mean by "averaged over distance." Velocity is, by definition, "total distance / total time" in the calculus sense of "total." By that definition, the puzzle is correct.
I admit that I might have thrown around the word "average" in a sloppy manner, so perhaps that’s what you meant? If so, you have a point — if you can point out exactly where the words are misused I could correct it. Thanks!
@Jason
When you average something like velocity, it must be in relationship to one of the two properties relating to it, time or distance.
Think auto racing. A car has an average lap time. That is not averaged over time, but averaged per lap. If I run one lap at 30 mph and one a 90 mph, my average lap time for those two laps would be 60 mph ((30 + 60) / 2). Averaged over time, it would be 40 mph (I spend twice as long at 30 mph than I do at 60 mph, so ((30 x 2 + 60) / 3) = 40
Make sense?
Just exercising my MIT eduation ;-)
@Kyle: I do see your point.
I think you meant that average lap speed over distance would be ((30 + 90)/2) = 60, and over time would be ((30*3 + 90) / 4 = 45. But of course I understand your argument.
So you’re right about the wording of the word problem, but I think the end result is the same, because in "productivity" you’re definitely interested in "total work done in total amount of time," and not some kind of "lap average."
This is what I get for taking a dig at MIT grads. :-)
(Actually, it’s awesome! Thanks!)
Jason,
Your MIT education was money well spent!!! This is so brilliant:
Once you’re behind, you can’t make up ground no matter how fast you go.
It’s so good, I logged into yet another TIME SUCK device (twitter) to Tweet this!!!
I ADORE the "low velocity" activity metaphor! BRILLIANT!!! (Your mother must be proud!)
I wish I’d had friends like YOU when I was wasting my college money – er, um, I mean acquiring a college degree. If I’d been able to GRASP this concept, I wouldn’t have found myself on high risk insurance while I waited for all those tickets to "drop" off my record!!
@Kathy: Oh no, I didn’t go to MIT, I just figured that those who did would jump on it, and indeed it appears they have. :-) (P.S. At Smart Bear I can always count on our resident MIT alum to bang out this kind of stuff.)
Thanks as always for your cheery comments! You’re always the highlight of the day. :-)
I have to say I really like Lin’s concept of improving 1% per day but your post definitely sheds a new light to my own productivity. Email seems to be my worse time suck these days! Not sure if I can do anything about it… Any ideas?
I think the issue is you hafta average an incremental 1% every day… I think that’s really hard because there’s also forces that are causing it to go down, so you hafta battle those days.
The accuracy of the math notwithstanding, your analogy is great… basically you’re better off doing a little every day instead of going in major spurts.
The other thing I like is you only hafta cut down a little of your wasteful time at a time… or on the other hand, increase you good stuff a little at time. And then it compounds.
I was asked this 60 mph question in an interview with Microsoft back in college.
@Jason
You realize you improved your speed an infinite % when you started up your car and it went from rest (0 mph) to driving 30 mph in your fun example. So relatively, 37x isn’t impossible. In fact, it doesn’t seem too hard. ;-) Besides, we like to do the impossible at Zappos. We were told all the time that it was impossible to sell shoes, clothing, and handbags on the internet. :-)
Anyway, taking things to mathematical extremes may not always make much sense, as your MIT education have taught you. Just to be clear on my post, I was trying to inspire our employee to start the year off on the right foot and to do things they wanted to do for a while but thought were impossible and / or have never tried. It is more important to just get started and improved every single day. In these kinds of new initiatives, it is completely possible to improve 37x over a year. In fact, 37x might even be a low bar. For example, over the past year, @zappos (Tony Hsieh, our CEO) grew his twitter following from 100 (at last year’s SXSW conference) to over 220,000 (as of today). That’s over 2200x. It is true that certain conditions have to be true for my math example to work. The measurement scale being used has to be continuous and infinite. It is also true that improvements are unlikely to be precisely compounded daily by 1%. The math I did was to illustrate the point 37x improvement over a year is possible, when everyone thinks it is too high of a bar or impossible.
BTW, I completely agree with your post that low-velocity activities kill productivity. The question then is if you reduced or eliminated your low-velocity activities and reallocated that time to high-velocity activities, maybe you can’t be 37x more "productive" (because time is on a finite scale for any given time period) but the question is over a year time frame could you be 37x more "effective" (measured by whatever effectiveness metric on an infinite scale that you are trying to achieve) . I think that is certainly doable, as @zappos was able to demonstrate with the growth of his twitter following.
All in all, I believe we agree but are looking at things from two very different perspectives. Effective people are constantly trying to reduce time spent on low value tasks, reallocate time to high value projects, and constantly improving on their high value abilities.
Thanks for you post! I really enjoyed it and did give me a fresh new perspective.
@Alfred
Thanks so much for responding! It’s great to hear your side of things.
I think your example of growing Twitter subscribers by 2000x is not the same thing as increasing productivity 37x.
Answering 37x more tech support emails would a productivity increase, but I don’t think you’d expect any of your employees to accomplish that by the end of the year, or ever for that matter.
Handling 37x more orders without new warehousing and without hiring anyone new would be a productivity increase, but that’s a silly expectation too.
Sometimes 37x increases are possible, but by break-the-world processes, not by 1% improvements. For example, email has made communication by notes more than 37x more efficient, but it didn’t happen because of 1% improvements over pen, paper, and horse.
At the end of the day, however, it’s clear we agree on the main points: That you should always be looking to optimize yourself, and that low-velocity tasks can drag us down more than we realize.
Thanks again!
Surprised to not have seen in the article or comments that although 1.01^365 days does equal 37.8, 1.01^((52-2)*5) = 12.03.
In other words, the real insight about this zappos place is that all the employees are required to work 7 days a week with no breaks or holidays, and improve things every one of those days no matter how exhausted they are working this schedule.
@Scott — Ha, that’s true! And as you point out, taking out days massively changes the exponential function.
To be fair, although he talked about Zappos, I think the idea was giving advice to be used in your personal life as well.
In any case, great catch! Some future posts will have more math, so I’ll look to you to keep me straight. :-)
How to make Zappos better=quit charging me more for Puma shoes than Puma charges. Your returns aren’t free. Your extra cost pays for all the idiots who can’t decide what kind of shoes they want.
Sorry, I just had to get that out there.
And having lots of Twitter followers means nothing to business productivity or results. Oprah has over 800 000 followers, but it doesn’t mean she has started saying things of value yet, does it…
Innovation and creativity are clearly the by-products of the work environment you place yourself in each day. When your assets are intellectual property it is even more important that you invest in a home work environment that generates as much innovation and creativity as possible. Once I decided to purchase modular office furniture for my home office my business has been on a very positive trajectory.
I can’t believe I’m taking the time to type this, but…
Jason, you were right to begin with. Speed is a rate, and the only meaning of average rate is change in variable over time (variable being distance traveled or position in this case). To the extent that there’s any such thing as an average speed over distance, "average speed" is not a label for it.
It’s not a particularly useful or natural construct, either. Lap times are *not* an example of velocity over distance actually used anywhere in the real world, because lap times are *times*, not speeds. Add your lap times together, divide by the total number of laps and you’ve got laps per time–a measurement of (average) speed.
@Joshua — You’re making a common mistake! If you average lap times you get "average lap time" but that is NOT the same as "average speed."
This is because "speed" is by definition velocity, and you cannot average velocities in this manner.
If you look online or in a physics textbook you will always find "speed" equated with "velocity," and everywhere you will find word problems that take advantage of the misconception of the definition of "average velocity" you are describing.
I’m tripling my lameness by returning to a dead thread to defend myself when I was only backing up the author to begin with, but…
1) Speed != Velocity. Check your physics book again, or consult wikipedia. <http://en.wikipedia.org/wiki/Speed>. Speed is the scalar component of velocity. (The other component is direction: velocity is a vector.) As such, it *is* meaningful to talk about an average speed even if you were just driving round and round in an oval anyway.
(You can average velocities driving around an oval, too. It’s just that if you end up back where you started, your velocities all cancel out and you average zero no matter how long you drove.)
I allowed speed and velocity to be semi-interchangeable in my first comment because your example was about speeds (mph), but you went on to use the word "velocity". In my comment and in your post we both were using "velocity" to mean "speed", though that’s not quite true. It’s only colloquially that speed == velocity, definitely not in physics books.
2) Average lap time is indeed a measure of speed. To use totally bogus numbers, an average lap time of 2:30 means a speed of 1 lap per 2.5 minutes. If a lap is 1/2 mile, we easily can do the math to convert to more familiar units: 12 miles per hour. (If you want to get into how the actual distance driven in a lap may vary depending on position, etc., that’s true, but it only means our speed measurement isn’t very precise.)
“Here’s the mythical eight-hour workday quantified — I’m starting with 5-6 and even then I spent much of it fielding email.”
I realised how short the work day really is when reading the now habit.
Following the advice of the book, I now do actual work no more than 5 hours a day (and that does NOT include email sorting, which takes around 30 minutes avery day). You can read more on my blog.
.-= jrduboc’s latest blog post: Ubuntu =-.